Definición:
El método de Lin Bairstow es un método iterativo, basado en el método de Müller y de Newton Raphson. Dado un polinonio fn(x) se encuentran dos factores, un polinomio cuadrático f2(x) = x2 – rx – s y fn-2(x). El procedimiento general para el método de Lin Bairstow es:
El método de Lin Bairstow es un método iterativo, basado en el método de Müller y de Newton Raphson. Dado un polinonio fn(x) se encuentran dos factores, un polinomio cuadrático f2(x) = x2 – rx – s y fn-2(x). El procedimiento general para el método de Lin Bairstow es:
- Dado fn(x) y r0 y s0
- Utilizando el método de NR calculamos f2(x) = x2 – r0x – s0 y fn-2(x), tal que, el residuo de fn(x)/ f2(x) sea igual a cero.
- Se determinan la raíces f2(x), utilizando la formula general.
- Se calcula fn-2(x)= fn(x)/ f2(x).
- Hacemos fn(x)= fn-2(x)
- Si el grado del polinomio es mayor que tres regresamos al paso 2
- Si no terminamos
La principal diferencia de este método, respecto a otros, es que permite calcular todas las raíces de un polinomio (reales e imaginarias).
Para calcular la división de polinomios, hacemos uso de la división sintética. Así dado
fn(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0
Al dividir entre f2(x) = x2 – rx – s, tenemos como resultado el siguiente polinomio
fn-2(x) = bnxn-2 + bn-1xn-3 + … + b3x + b2
con un residuo R = b1(x-r) + b0, el residuo será cero solo si b1 y b0 lo son.
Los términos b, los calculamos utilizamos división sintética, la cual puede resolverse utilizando la siguiente relación de recurrencia
bn = an
bn-1 = an-1 + rbn
bi = ai + rbi+1 + sbi+2
Una manera de determinar los valores de r y s que hacen cero el residuo es utilizar el Método de Newton-Raphson. Para ello necesitamos una aproximación lineal de b1 y b0 respecto a r y s la cual calculamos utilizando la serie de Taylor
donde los valores de r y s están dados y calculamos los incrementos dr y ds que hacen a b1(r+dr, s+ds) y b0(r+dr, s+dr) igual a cero. El sistema de ecuaciones que tenemos que resolver es:
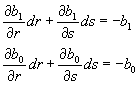
Bairtow muestra que las derivadas parciales se pueden obtener haciendo un procedimiento similar a la división sintética, así
cn = bn
cn-1 = bn-1 + rcn
ci = bi + rci+1 + sci+2
Ejemplo 1
Dado el polinomio f5(x) = x5 - 3.5x4 + 2.75x3 + 2.125x2 - 3.875x + 1.25, determinar los valores de r y s que hacen el resido igual a cero. Considere r0 = -1 y s0 = 2.
Solución.
Iteración 1
La división sintética con el polinomio f2(x) = x2 -x + 2.0 da como resultado
f3(x) = x3 - 4.5x2 + 9.25x - 16.125 Residuo = {30.75, -61.75}
Aplicando el método de Newton tenemos
-43.875
|
16.75
|
dr
|
-30.75
| ||
108.125
|
-43.875
|
ds
|
61.75
|
de donde
r1 = -1.0 + 2.7636812508572213 =1.763
s1 = 2.0 + 5.403374022767796 =7.403
Iteración 2
La división sintética con el polinomio f2(x) = x2 -1.763x - 7.403 da como resultado
f3(x) = x3 - 1.736x2 + 7.091x - 1.776
Residuo = {51.756, 105.685}
Aplicando el método de Newton tenemos
27.628
|
14.542
|
dr
|
-51.756
| ||
208.148
|
27.628
|
ds
|
-105.685
|
de donde
r2 = 1.7636 - 0.047 = 1.716
s2 = 7.403 - 3.469 = 3.934
Iteración 3
La división sintética con el polinomio f2(x)= x2 - 1.716x - 3.934 da como resultado
f3(x) = x3 - 1.783x2 + 3.622x + 1.326
Residuo = {12.654, 28.188}
Aplicando el método de Newton tenemos
13.834
|
7.441
|
dr
|
-12.654
| ||
65.679
|
13.834
|
ds
|
-28.188
|
de donde
r3 = 1.716 - 0.116 = 1.599
s3 = 3.934 - 1.483 = 2.450
En resumen,
k
|
r
|
s
|
Residuo
| |
0
|
-1
|
2
|
30.75
|
-61.75
|
1
|
1.763
|
7.403
|
51.756
|
105.685
|
2
|
1.716
|
3.934
|
12.654
|
28.188
|
3
|
1.599
|
2.450
|
2.899
|
8.154
|
4
|
1.333
|
2.186
|
0.760
|
2.522
|
5
|
1.118
|
2.113
|
0.271
|
0.607
|
6
|
1.027
|
2.023
|
0.043
|
0.111
|
7
|
1.001
|
2.001
|
0.002
|
0.006
|
8
|
1.000
|
2.000
|
1.139E-5
|
2.675E-5
|
La solución es:
f3(x) = x3 - 2.53x2 + 2.25x - 0.625 y f2(x) = x2 - x - 2
Las raíces de f2(x) = x2 - x - 2, son
x1 = 2
x2 = -1
Si repetimos el ejemplo pero ahora considerando el polinomio f3(x) = x3 - 2.53x2 + 2.25x - 0.625 , podemos calcular el total de las raíces del polinomio original.
No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.