M. Directos

Definición:

Los métodos directos son aquellos que determinan la solución en un numero determinado de pasos.

Para los métodos directos se preferirá un sistema cuya matriz de coeficientes sea simétrica y definida positiva. Una matriz A es simétrica si su transpuesta es igual a A.

Clasificación :

• Métodos de reducción: Método de eliminación de Gauss y Método de Gauss-Jordan.
• Métodos de factorización: Método de Crout, Método de Doolittle y Método de Cholesky.

Método de Eliminación de Gauss

En forma general, este método propone la eliminación progresiva de variables en el sistema de ecuaciones, hasta tener sólo una ecuación con una incógnita. Una vez resuelta esta, se procede por sustitución regresiva hasta obtener los valores de todas las variables.

El método de Gauss consiste en utilizar el método de reducción de manera que en cada ecuación tengamos una incógnita menos que en la ecuación precedente.

• Ejemplo: RESUELVA,

           

Ponemos como primera ecuación la que tenga el como coeficiente de x: 1 ó -1, en caso de que no fuera posible lo haremos con y o z, cambiando el orden de las incógnitas.

           

Hacemos reducción con la 1ª y 2ª ecuación, para eliminar el término en x de la 2ª ecuación. Después ponemos como segunda ecuación el resultado de la operación:

       E'₂ = E₂ − 3E₁

           

Hacemos lo mismo con la ecuación 1ª y 3ª ecuación, para eliminar el término en x.

       E'₃ = E₃ − 5E₁

           
            

Tomamos las ecuaciones 2ª y 3ª, trasformadas, para hacer reducción y eliminar el término en y.

        E''₃ = E'₃ − 2E'₂

               

Obtenemos el sistema equivalente escalonado.

           

Encontrar las soluciones.

    z = 1
    − y + 4 · 1 = −2        y = 6
    x + 6 −1 = 1          x = −4

Método de Gauss-Jordan

El Método de Gauss–Jordan  es un método por el cual pueden resolverse sistemas de ecuaciones lineales con n números de variables, encontrar matrices y matrices inversas.

Para resolver sistemas de ecuaciones lineales aplicando este método, se debe en primer lugar anotar los coeficientes de las variables del sistema de ecuaciones lineales en su notación matricial:

Entonces, anotando como matriz (también llamada matriz aumentada):

Una vez hecho esto, a continuación se procede a convertir dicha matriz en una matriz identidad, es decir una matriz equivalente a la original, la cual es de la forma:

Esto se logra aplicando a las distintas filas y columnas de las matrices simples operaciones de suma, resta, multiplicación y división; teniendo en cuenta que una operación se aplicara a todos los elementos de la fila o de la columna, sea el caso.

Para ilustrarnos mejor lo analizaremos con un ejemplo concreto:

• Sea el sistema de ecuaciones:

• Procedemos al primer paso para encontrar su solución, anotarlo en su forma matricial:

• Una vez hecho esto podemos empezar a operar con las distintas filas y columnas de la matriz para transformarla en su matriz identidad, teniendo siempre en cuenta la forma de la misma:

• Lo primero que debemos hacer es transformar el 2 de la 1ª fila de la matriz original en el 1 de la 1ª fila de la matriz identidad; para hacer esto debemos multiplicar toda la 1ª fila por el inverso de 2, es decir ½.

• Luego debemos obtener los dos ceros de la primera columna de la matriz identidad, para lograr esto, buscamos el opuesto de los números que se ubicaron por debajo del 1 de la primera columna, en este caso el opuesto de 3 que será -3 y el opuesto de 5 que será -5.

Una vez hecho esto, se procederá a multiplicar los opuestos de estos números por cada uno de los elemento de la 1ª fila y estos se sumaran a los números de su respectiva columna. 

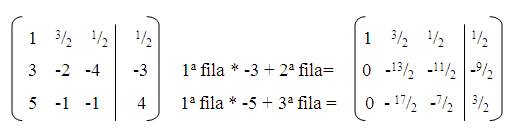
• Nuestro siguiente paso es obtener el 1 de la 2ª fila de la matriz identidad, y procedemos de igual forma que antes, es decir multiplicamos toda la fila por el inverso del numero que deseamos transformar en 1, en este caso -13/2, cuyo inverso es -2/13

Además si observamos la tercera fila, nos damos cuenta que todos los elementos poseen el mismo denominador, entonces podemos eliminarlos multiplicando todos los elementos de la 3º fila por 2 (el denominador).

• Ahora queremos obtener el 0 que se ubica en la 3ª fila, 2ª columna de la matriz identidad.

• A esta altura podemos observar como la matriz con la cual estamos operando empieza a parecerse a la matriz identidad.

Nuestro siguiente paso es obtener el 1 correspondiente a la 3ª fila, 3ª columna de la matriz identidad.

• Luego debemos obtener los dos ceros de la tercera columna de la matriz identidad.

Una vez hecho esto, se procederá a multiplicar los opuestos de estos números por cada uno de los elemento de la 3ª fila y estos se sumaran a los números de su respectiva columna. 

• El último paso que debemos realizar es obtener el 0 de la 1ª columna, 2ª fila de la matriz identidad.

• Como podemos observar hemos llegado al modelo de la matriz identidad que buscábamos, y en la cuarta columna hemos obtenido los valores de las variables, correspondiéndose de este modo:

x= 1

y= -1

z= 2

• Luego, el sistema de ecuaciones está resuelto y por último lo verificamos.

2x + 3y + z = 1 3x – 2y – 4z = -3 5x – y – z = 4

2*1+3*(-1)+2=1 3*1- 2*(-1)-4*2=-3 5*1-(-1)-2 =4

2 -3 +2 =1 3 +2 - 8= -3 5 +1 - 2 = 4

1 = 1 -3 = -3 4= 4